红黑树
1 规则定义
红黑树有以下五条性质:
1.节点是红色或者黑色的。
2.根节点的黑色的。
3.nil 节点时黑色的。
4.每个红节点的左子节点和右子节点必定是黑色的。(保证了两个红色节点不可能直接相连)
5.nil 节点在任意位置黑深度都相等。
任意一结点到每个叶子结点的路径都包含数量相同的黑结点。
(从nil节点开始,到达根节点,再去往不同的NIL节点,经过的黑节点数量相同
红黑树中的所有叶子节点到根节点的长度,在最坏情况下也不会大于最好情况下的两倍,所以红黑树就能保持「大致」的平衡。)
推论5.1:
任意一节点到每个叶子节点的路径都包含数量相同的 黑 节点
来自https://xieguanglei.github.io/blog/post/red-black-tree.html
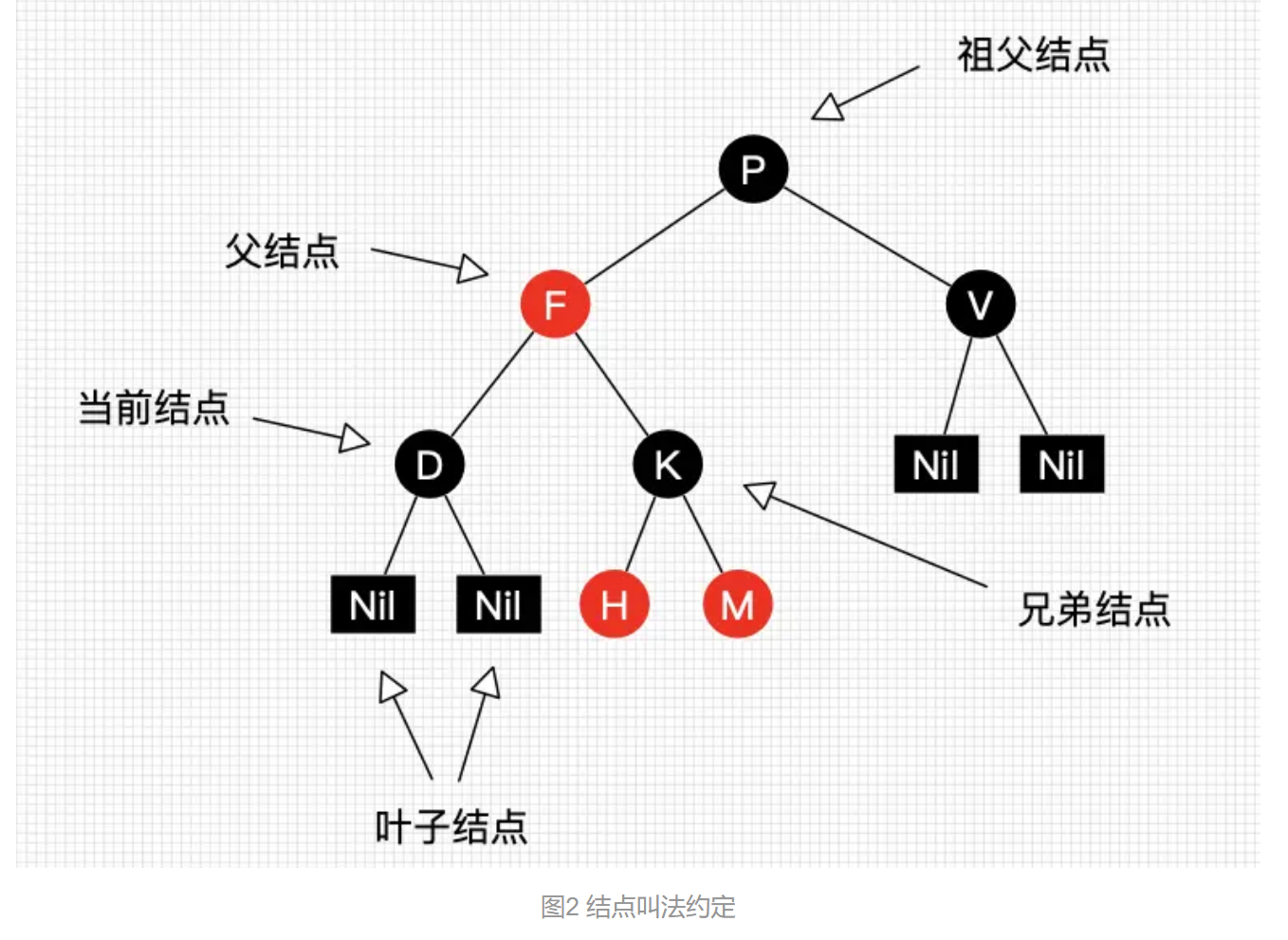
思考:
( 1 )nil 节点就是空节点,在红黑树的实现中,nil 节点代替二叉树中的 NULL
( 2 )叶子节点的左节点和右节点指针都指向nil 节点,只一个子树的节点,其另外一个子节点指针也指向nil 节点
( 3 )根节点的左右子树的黑高度都为n
( 4 )子树 塞满了红节点 ,再试图向其中插入节点,会导致树失去平衡
( 5 )如何在插入/删除后,保证树的 5 条性质?
1 、旋转
( 1 )左旋
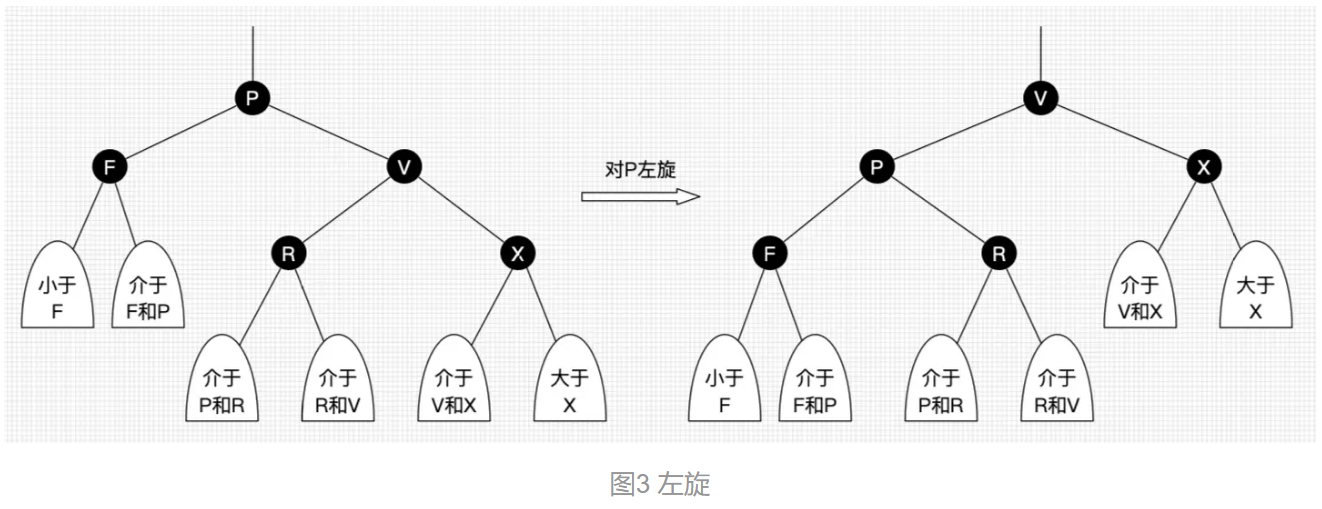
• 左旋:以某个结点作为支点(旋转结点),其右子结点变为旋转结点的父结点,右子结点的左子结点变为旋转结点的右子结点,左子结点保持不变。如图3。
( 2 )右旋
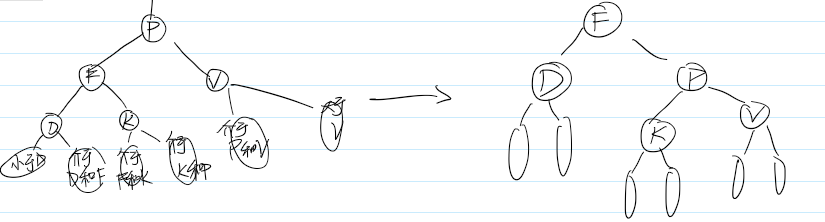
• 右旋:以某个结点作为支点(旋转结点),其左子结点变为旋转结点的父结点,左子结点的右子结点变为旋转结点的左子结点,右子结点保持不变。如图4。
来自<https://www.jianshu.com/p/e136ec79235c/>
( 3 )总结
旋转操作是 局部 的,不影响祖父节点。
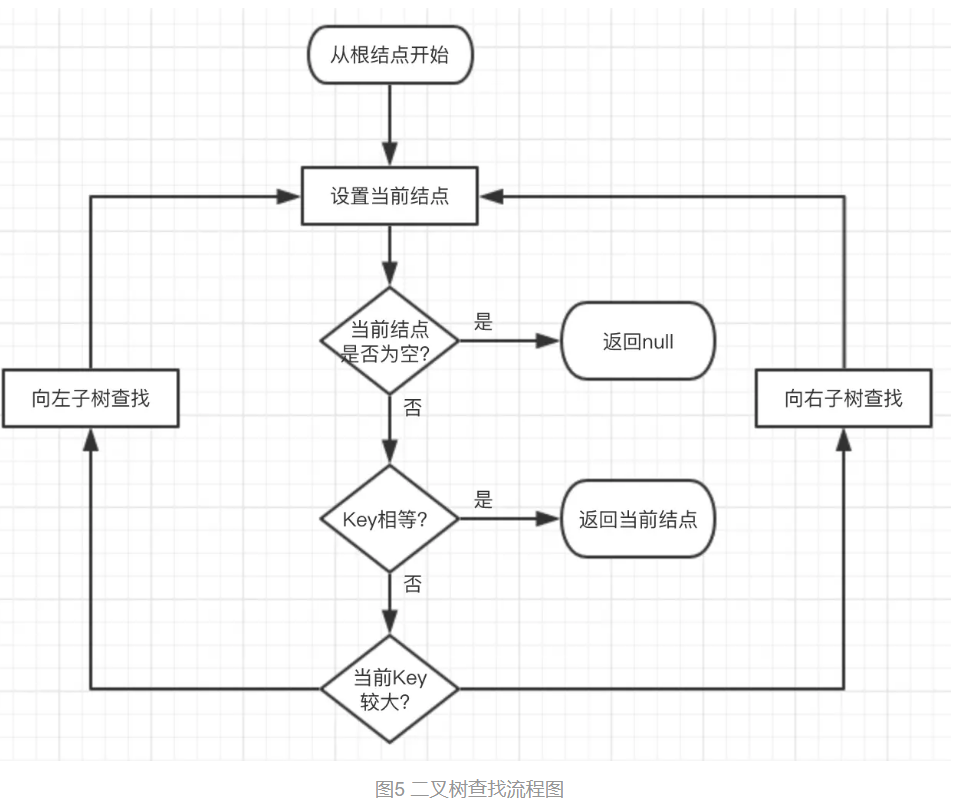
2 、查找
3 、插入
插入结点是应该是什么颜色呢?答案是红色。
理由很简单:
( 1 )红色在父结点(如果存在)为黑色结点时,红黑树的黑色平衡没被破坏,不需要做自平衡操作。
( 2 )但如果插入结点是黑色,那么插入位置所在的子树黑色结点总是多 1 ,必须做自平衡。
来自https://www.jianshu.com/p/e136ec79235c/
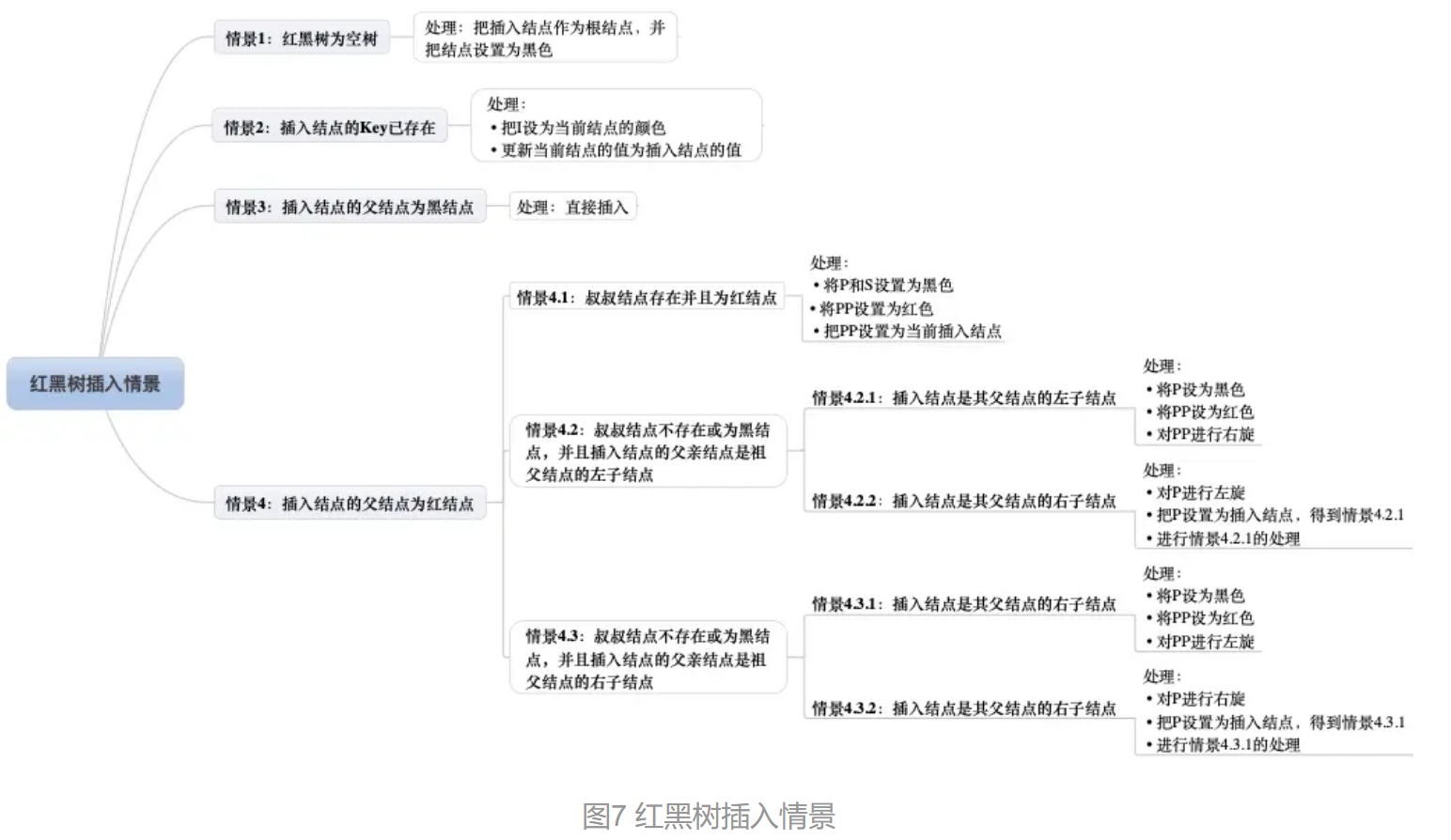
插入的情况分类
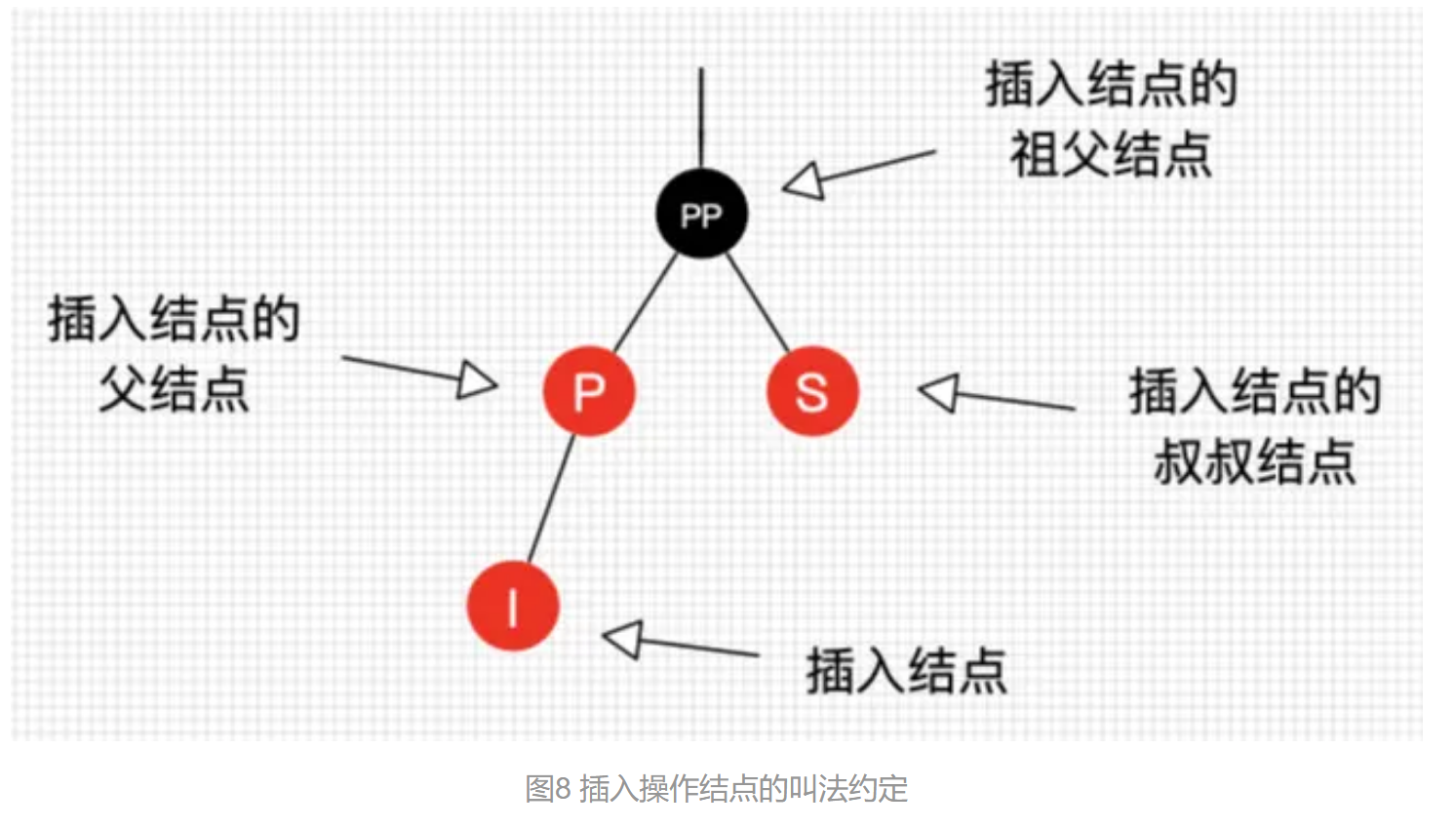
插入的命名规则
情景 1 :空树
情景 2 :插入节点的key已存在
替换颜色,更新节点的值
情景 3 :插入节点的父节点为黑节点
插入的节点是红色,父节点为黑节点,不影响平衡
情景 4 :插入节点的父节点为红节点
根节点是黑色,因此父节点不可能是根节点,后续旋转操作需要祖父节点的参与
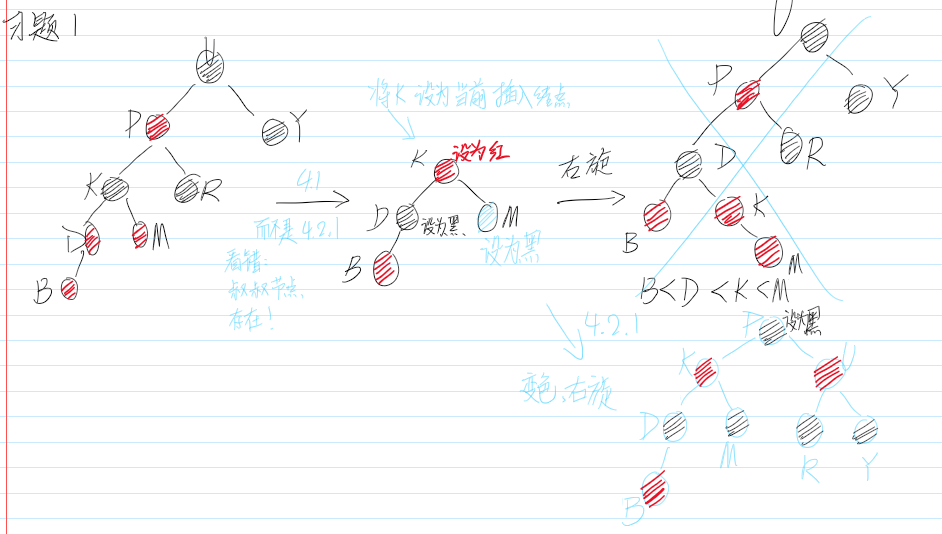
情景4.1:叔叔节点存在,且为红节点
该插入子树的红黑层数的情况是:黑红红
来自https://www.jianshu.com/p/e136ec79235c/
最简单的处理方式是把其改为:红黑红
来自https://www.jianshu.com/p/e136ec79235c/
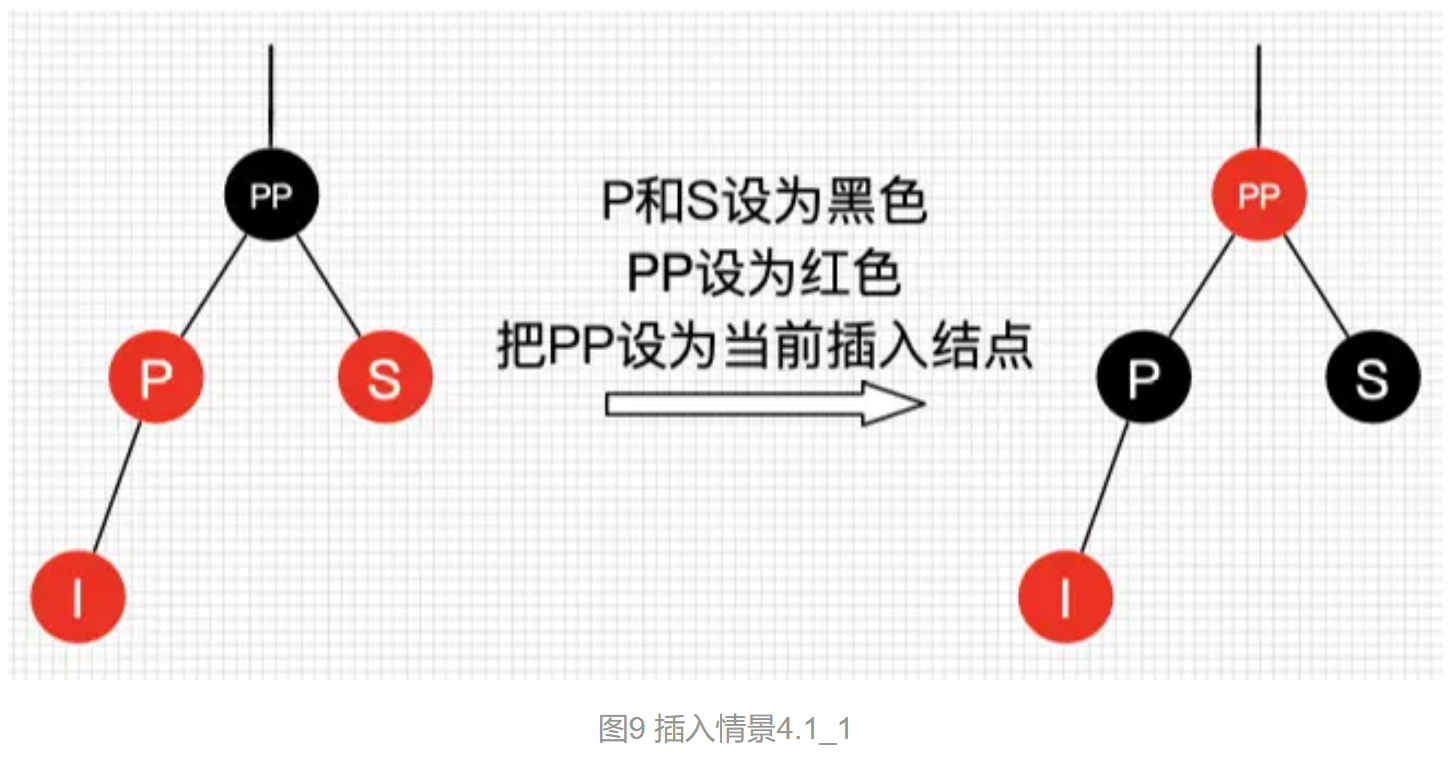
如果PP的父结点是黑色,那么无需再做任何处理;但如果PP的父结点是红色,则破坏了第 4 条规则
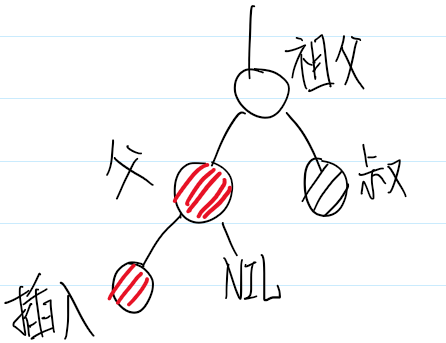
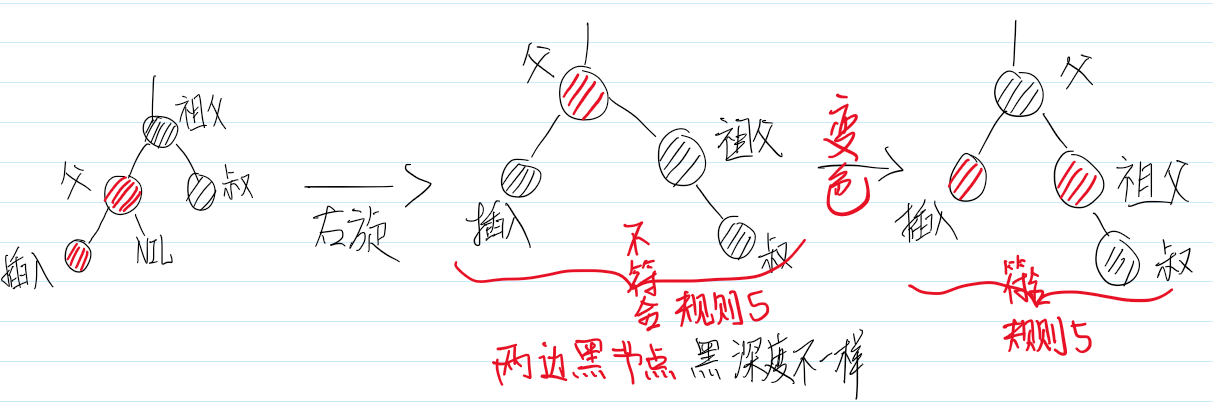
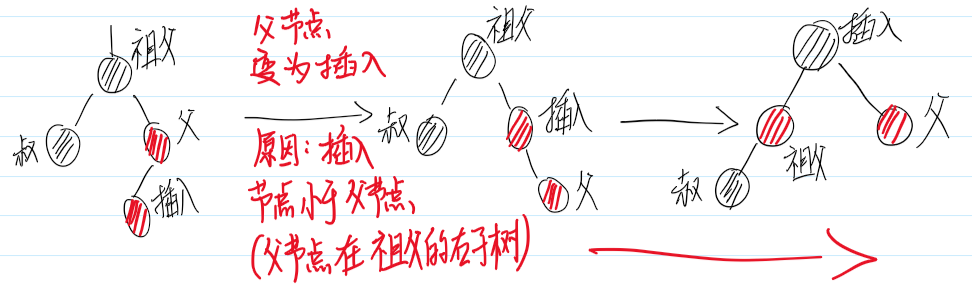
情景4.2:叔叔节点不存在/为黑色节点,并且插入节点的父亲节点是祖父节点的左子节点
叔叔结点 非红 即为叶子结点(Nil)。而父结点为红结点,那么叔叔结点所在的子树的黑色结点就比父结点所在子树的 多 了,这 不满足 红黑树的 性质 5 。
解决方法:
旋转。由于叔叔节点所在的子树的黑色节点比父节点所在子树多,因此,把叔叔节点所在子树的多的节点旋转到另一边
情景4.2.1:插入节点是父节点的左子节点

情景4.2.2:插入节点是父节点的右子节点
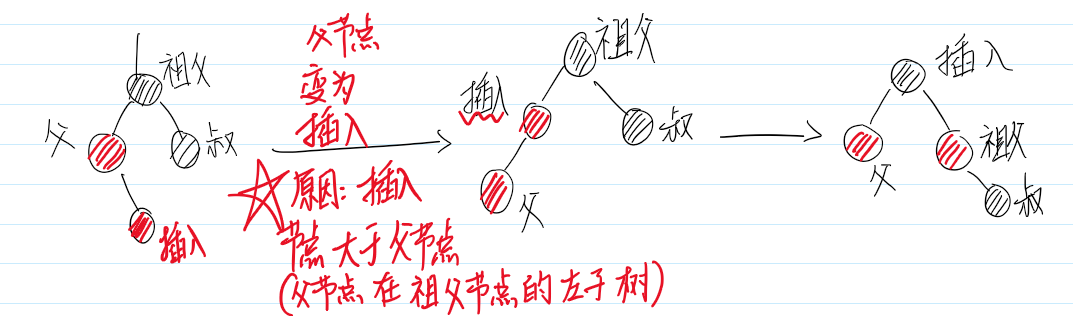
情景4.3:叔叔节点不存在或为黑节点,并且插入节点的父亲节点是祖父节点的右子树
情景4.3.1:插入节点是父节点的右子节点
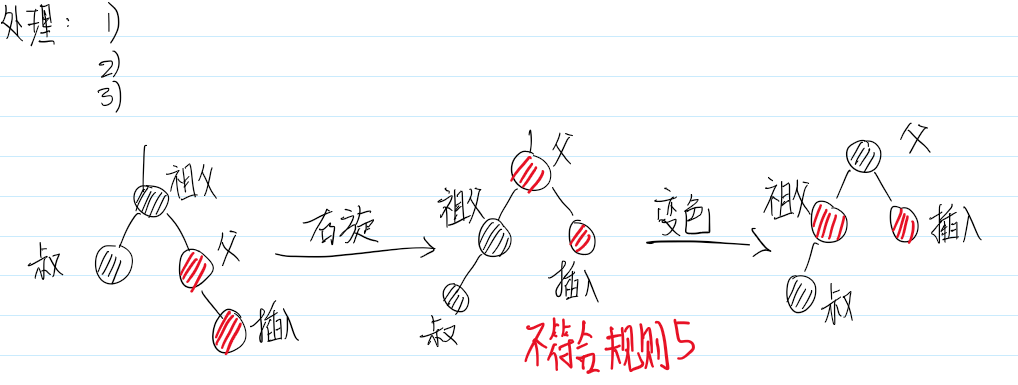
情景4.3.2:插入节点是父节点的左子节点
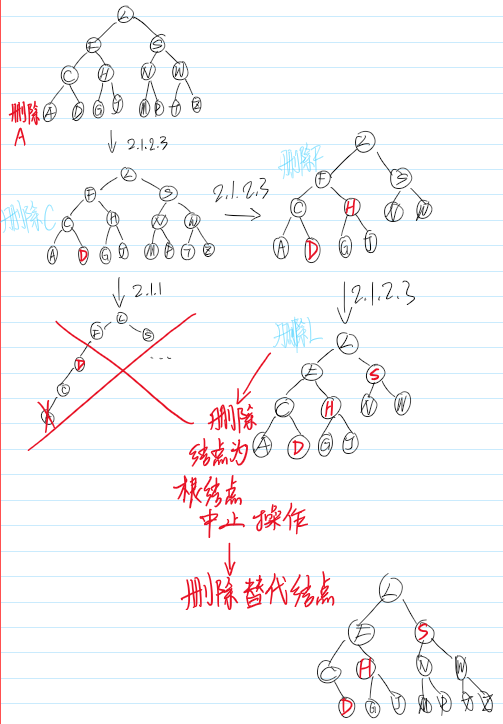
习题1-插入
4 、删除
红黑树的删除操作也包括两部分工作:
( 1 )
查找目标结点;而删除后自平衡。查找目标结点显然可以复用查找操作,当不存在目标结点时,忽略本次操作;当存在目标结点时,删除后就得做自平衡处理
( 2 )
删除了结点后我们还需要找结点来替代删除结点的位置,不然子树跟父辈结点断开了,除非删除结点刚好没子结点,那么就不需要替代。
二叉树删除结点找替代结点有3种情情景:
• 情景1:若删除结点无子结点,直接删除
• 情景2:若删除结点只有一个子结点,用子结点替换删除结点
- 情景3:若删除结点有两个子结点,用后继结点(大于删除结点的最小结点——删除结点的右子树种最左结点or 删除结点的右子树种最左结点)替换删除结点
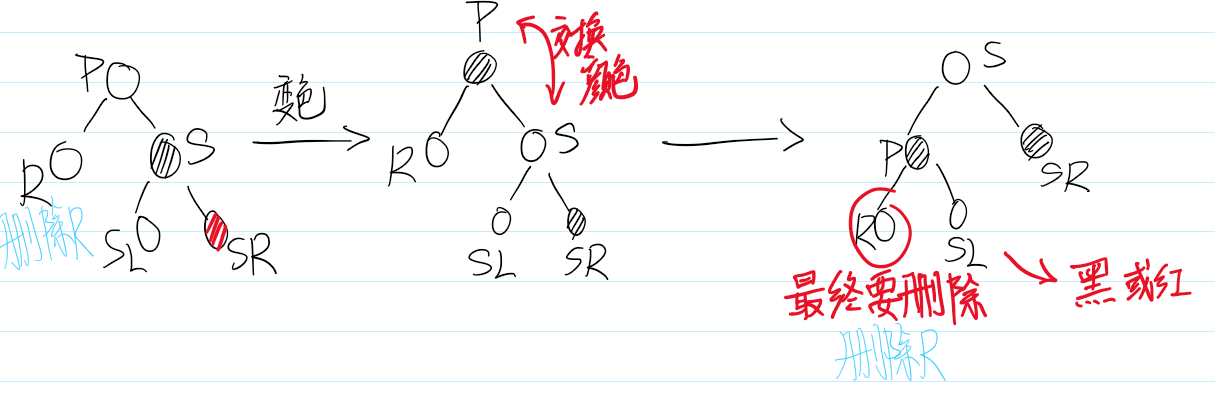
讲一个重要的思路:删除结点被替代后,在不考虑结点的键值的情况下,对于树来说,可以认为删除的是替代结点!
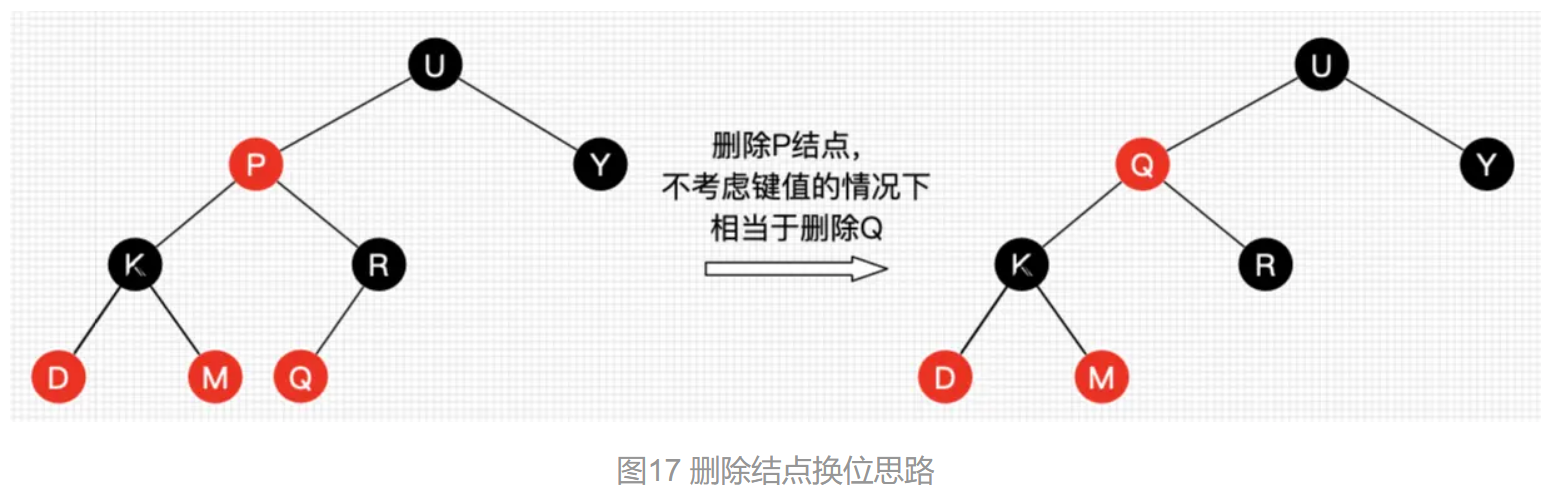
看图 17 。在不看键值对的情况下,图 17 的红黑树最终结果是删除了Q所在位置的结点!这种思路非常重要,大大简化了后文讲解红黑树删除的情景!
删除的情况分类
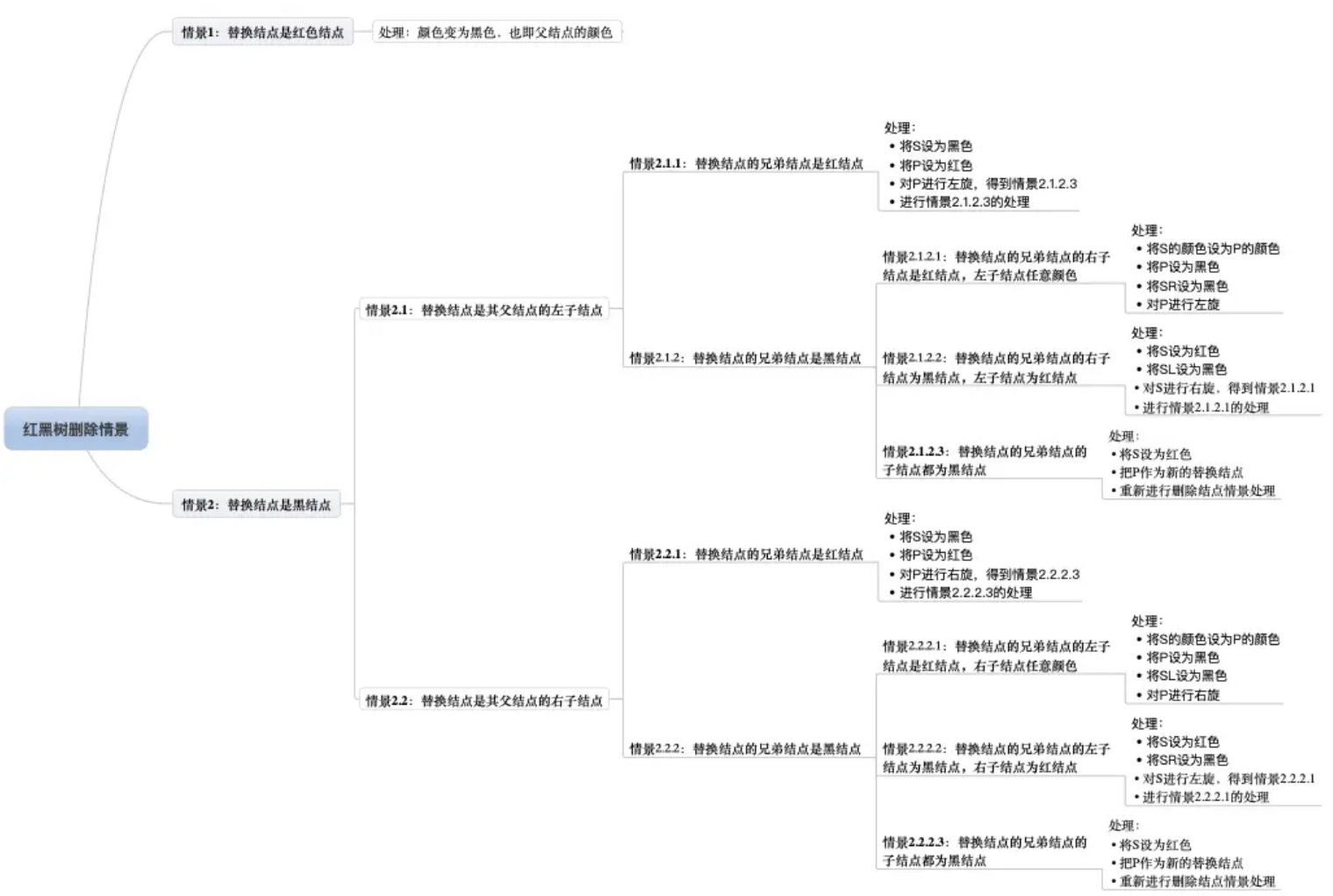
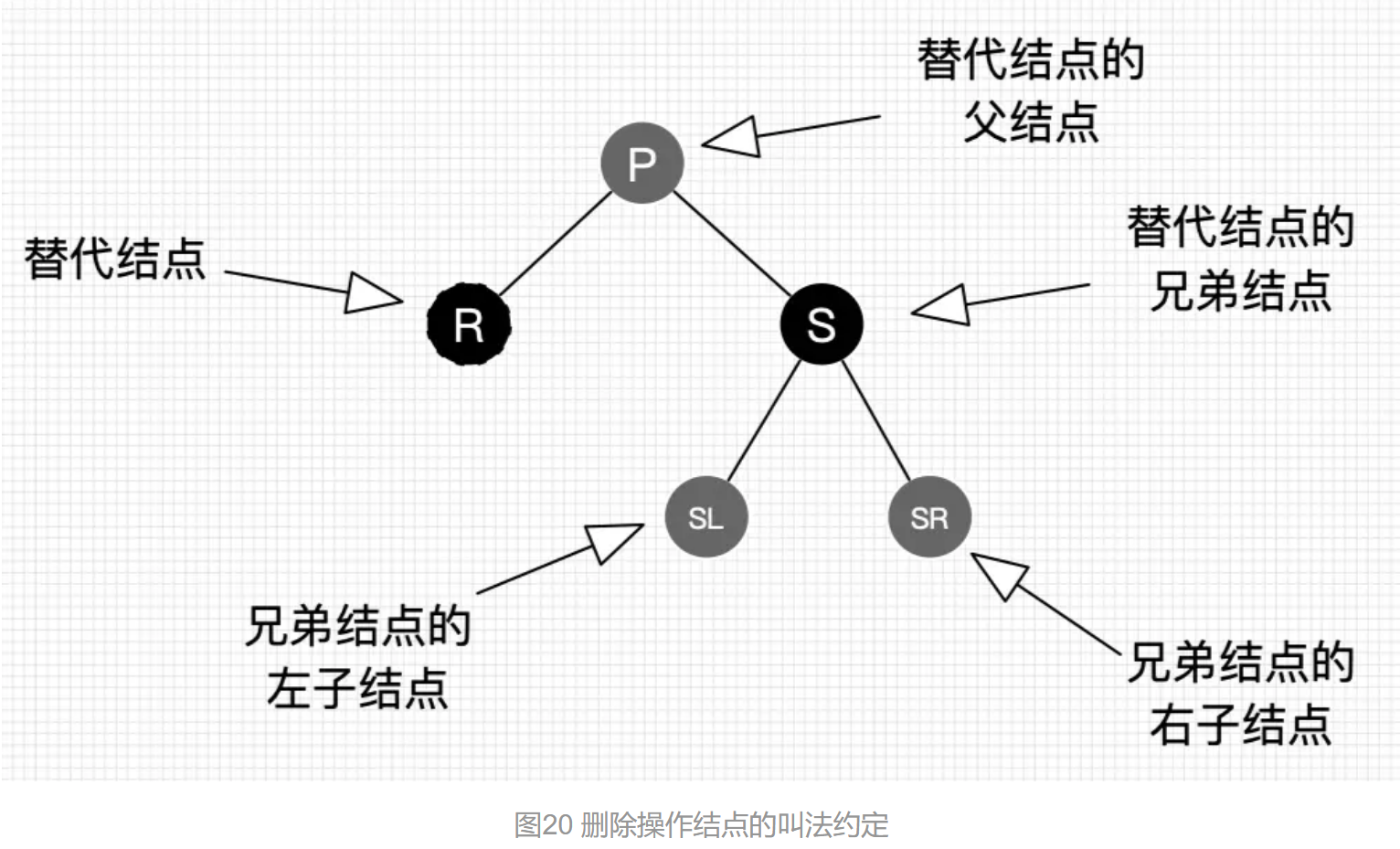
删除的命名规则
删除情景1:替换结点是红色结点
删除红色节点,不影响红黑树平衡
删除情景 2 :替换结点是黑结点
当替换结点是黑色时,我们就不得不进行自平衡处理
删除情景2.1:替换结点是父节点的左孩子
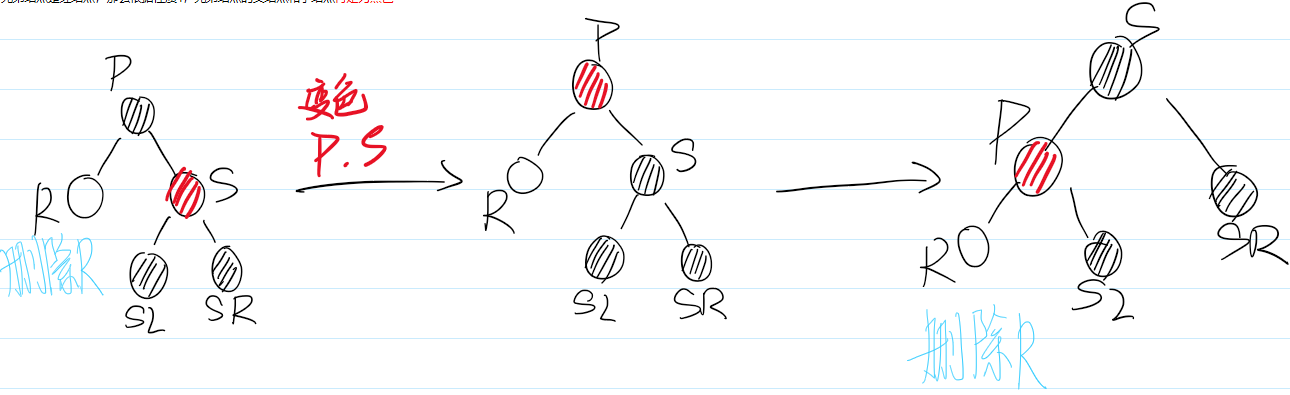
删除情景2.1.1:替换结点的兄弟节点是红色结点
若兄弟结点是红结点,那么根据性质 4 ,兄弟结点的父结点和子结点肯定为黑色
删除情景2.1.2:替换结点的兄弟节点是黑色结点
当兄弟结点为黑时,其父结点和子结点的具体颜色也 无法确定
删除情景2.1.2.1:兄弟结点的右子结点是红结点,左子节点任意颜色
删除情景2.1.2.2:兄弟结点的右子结点是黑结点,左子节点是红结点
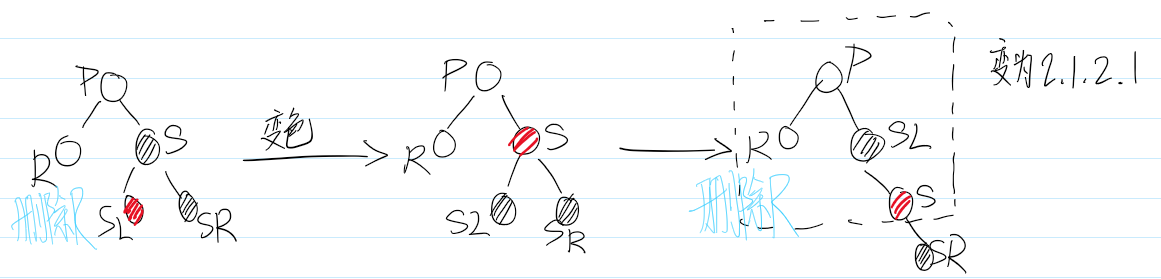
删除情景2.1.2.3:兄弟结点的子节点都是黑色
此次兄弟子树都没红结点“借”了,兄弟帮忙不了,找父母,这种情景我们把兄弟结点设为红色,再把父结点当作替代结点【很重要!删除节点指向了父结点】,自底向上处理
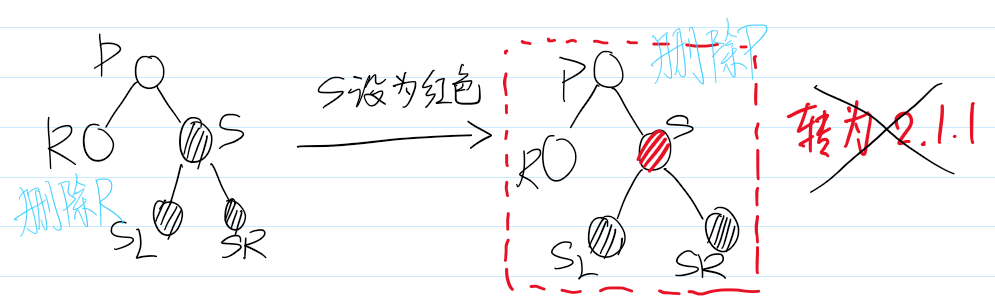
删除情景2.2:替换结点是父节点的右孩子
删除情景2.2.1:替换结点的兄弟节点是红色结点
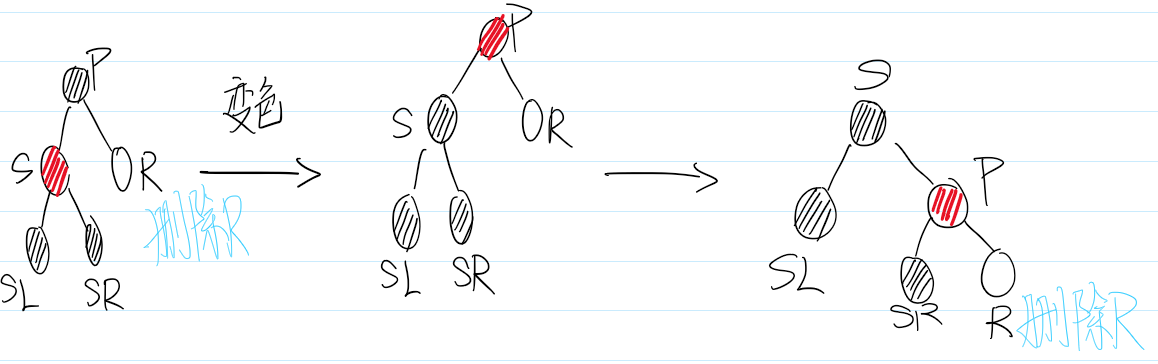
删除情景2.2:替换结点是父节点的右孩子
删除情景2.2.1:替换结点的兄弟节点是红色结点
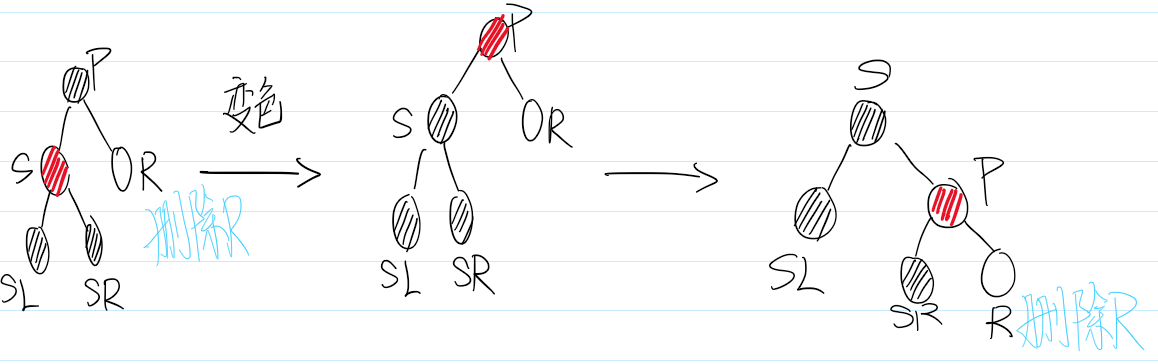
删除情景2.2.2:替换结点的兄弟节点是黑色结点
删除情景2.2.2.1:兄弟节点的左子节点是红,右子节点任意颜色
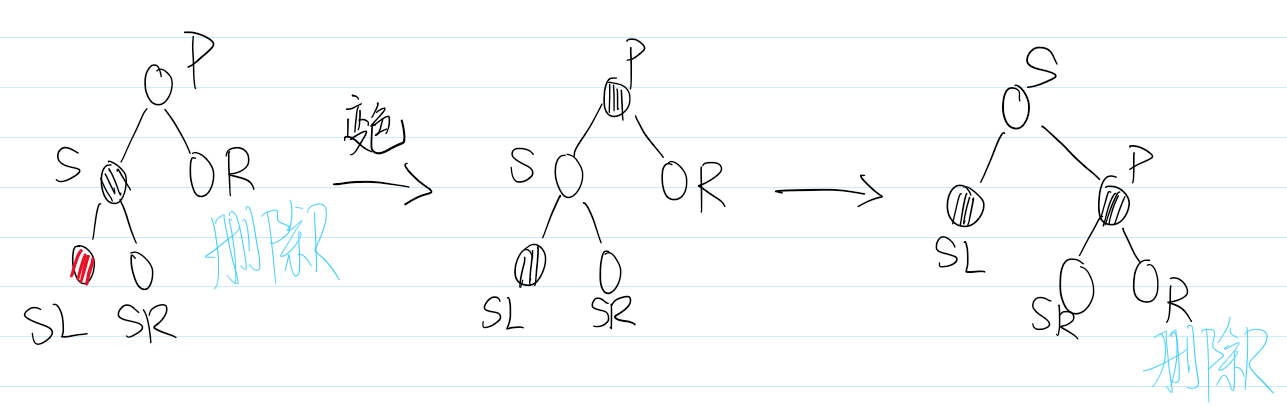
删除情景2.2.2.2:兄弟节点的左子节点是黑色结点,右子节点是红
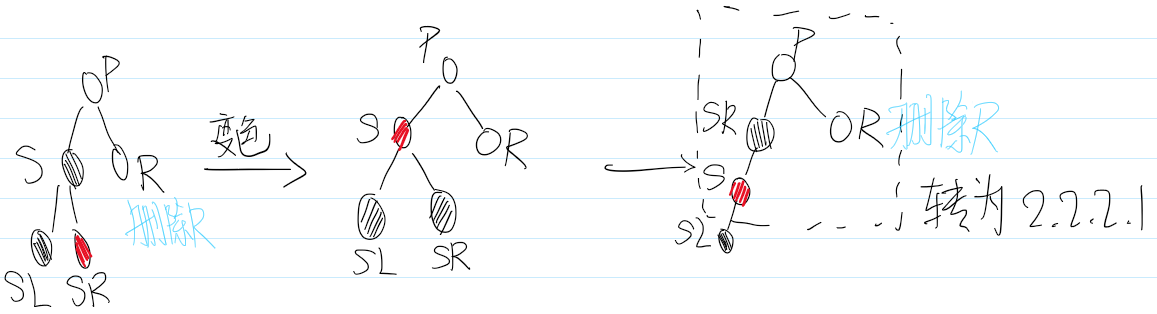
删除情景2.2.2.3:兄弟节点的子节点是黑色结点
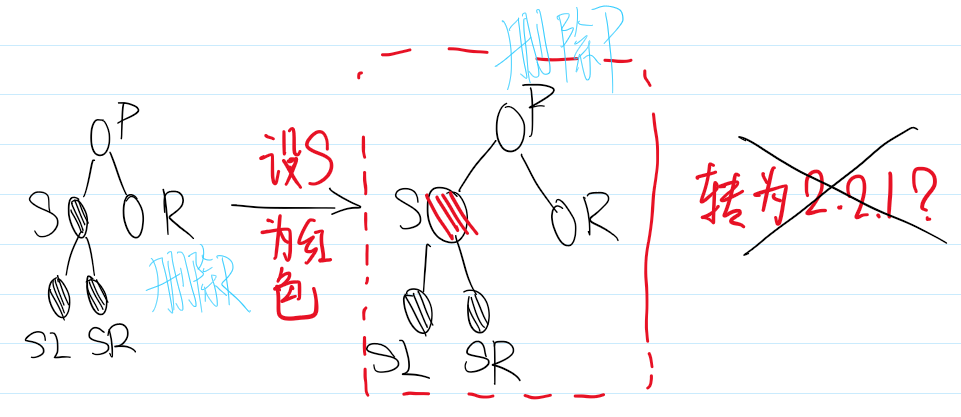
删除总结
红黑树删除后自平衡的处理可以总结为:
1.自己能搞定的自消化(情景1)
2.自己不能搞定的叫兄弟帮忙(除了情景1、情景2.1.2.3和情景2.2.2.3)
3.兄弟都帮忙不了的,通过父母,找远方亲戚(情景2.1.2.3和情景2.2.2.3)
来自<https://www.jianshu.com/p/e136ec79235c/>
习题2-删除